반응형
SymPy 라이브러리 가져오기
# Importing Library
import sympy기호 정의
# Defining Symbols
x = sympy.Symbol("x")
y = sympy.Symbol("y")방정식 작성
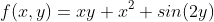
# Creating Equation
f = x * y + x ** 2 + sympy.sin(2 * y)미분
# Differentiate wtr x
df_dx = sympy.diff(f, x)
print("The derivative of f(x,y) wrt x is: " + str(df_dx))The derivative of f(x,y) wrt x is: 2*x + y# Second Derivative wrt y
d2f_dy2 = sympy.diff(f, y, 2)
print("The 2nd derivative of f(x,y) wrt y is: " + str(d2f_dy2))The 2nd derivative of f(x,y) wrt y is: -4*sin(2*y)통합
# Integrate wrt x
F = sympy.integrate(f, x)
print("The integral of f(x,y) wrt x is: " + str(F))The integral of f(x,y) wrt x is: x**3/3 + x**2*y/2 + x*sin(2*y)# Definite Integral wrt x [0, 2]
F = sympy.integrate(f, (x, 0, 2))
print("The definite integral of f(x,y) wrt x with bounds [0, 2] is: " + str(F))The definite integral of f(x,y) wrt x with bounds [0, 2] is: 2*y + 2*sin(2*y) + 8/3SymPy의 기타 유용한 기능
- 단순화는 방정식을 더 간단한 형태로 줄이는 데 사용할 수 있는 훌륭한 함수이다. 예를 들어, 다음과 같은 방정식을 줄일 수 있다.
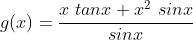
# Simplifying Equations
g = (x * sympy.tan(x) + x ** 2 * sympy.sin(x))/sympy.sin(x)
g = sympy.simplify(g)
print("The simplified form of g(x) is: " + str(g))The simplified form of g(x) is: x*(x + 1/cos(x))- 풀이는 대수 방정식의 시스템을 푸는 데 사용할 수 있는 또 다른 위대한 함수이다. 해법 함수를 사용하기 위해서는 변 중 하나가 0이 되도록 방정식의 체계를 조정할 필요가 있습니다. 그러면 우리는 아래와 같이 해결 함수를 사용하여 x와 y에 대한 답을 얻을 수 있습니다. 다음의 방정식이 있다고 가정하자.
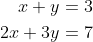
# Solving System of Equations
sol = sympy.solve((x + y - 3, 2 * x + 3 * y - 7), (x, y))
print("The solution of the system is (x, y): (" + str(sol[x]) + ", " + str(sol[y]) + ")")The solution of the system is (x, y): (2, 1)'프로그래밍' 카테고리의 다른 글
| 직원들이 원하는 건 다 줬어요 그들은 옆구리를 치고 떠났다. (0) | 2022.02.15 |
|---|---|
| 내 상사가 잘못된 프로젝트 일정 추정으로 프로그래머를 해고하는 8가지 이유 (0) | 2022.02.15 |
| IT 업계에서 가장 큰 거짓말은 무엇입니까? (0) | 2022.02.15 |
| Python 강화 제안에서 제공하는 향후 Python 기능 (0) | 2022.02.15 |
| 메소드의 아름다움 에러 (0) | 2022.02.15 |




댓글